2020年人教版高中选修1-1数学期末模拟试题
1、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目需要的
1.命题“![]() ”的否定是()
”的否定是()
A.∀x∈R,![]() B.∀x∈R,lnx0
B.∀x∈R,lnx0![]()
C.![]() D.
D.![]()
2.抛物线y2=﹣x的焦点坐标为()
A.(![]() ,0) B.(
,0) B.(![]() ,0) C.(
,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
3.命题“若a+b>1,则a2+b2>1”的逆否命题为()
A.若a2+b2≤1,则a![]() +b≤1 B.若a2+b2>1,则a+b>1
+b≤1 B.若a2+b2>1,则a+b>1
C.若a+b>1,则a2+b2≤1 D.若a2+b2<1,则a+b<1
4.设f(x)是可导函数,当h→0时,![]() ,则f'(x0)=()
,则f'(x0)=()
A.2 B.![]() C.﹣2 D.
C.﹣2 D.![]()
5.已知焦点在y轴上的椭圆![]() 1(a>0)的焦距为4
1(a>0)的焦距为4![]() ,则该椭圆的长轴长为()
,则该椭圆的长轴长为()
A.4 B.8 C.2 D.2![]()
6.某跳水运动员离开跳板后,他达到的高度与时间的函数关系式是h(t)=10﹣4.9t2+8t(距离单位:米,时间单位:秒),则他在0.5秒时的瞬时速度为()
A.9.1米/秒 B.6.75米/秒 C.3.1米/秒 D.2.75米/秒
7.已知函数f(x)=x3+ax2+(a+6)x﹣3有两个极值点,则实数a的取值范围是()
A.(﹣3,6) B.(﹣∞,﹣3]∪[6,+∞)
C.[﹣3,6] D.(﹣∞,﹣3)∪(6,+∞)
8.![]() a≥5是命题“∀x∈[1,2],x2﹣a≤0”为真命题的()
a≥5是命题“∀x∈[1,2],x2﹣a≤0”为真命题的()
A.充分而非必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也非必要条件
9.若双曲线mx2﹣y2=1(m>0)的一条渐近线与直线y=﹣2![]() x垂直,则此双曲线的离心率为()
x垂直,则此双曲线的离心率为()
A.2 ![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设函数f(x)![]() 在概念域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能为()
在概念域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能为()

A.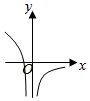 B.
B.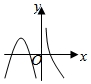
C.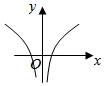 D.
D.
11.若函数f(x)在R上可导,且f(x)<xf'(x),则()
A.ef (1)<f(e) B.ef(1)>f(e)
C.ef (1)=f(e) D.f(1)=f(e)
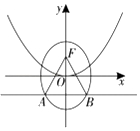
12.已知抛物线x2=4y的焦点F是椭圆![]() 1(a>b>0)的一个焦点,且该抛物线的准线与椭圆相交于A、B两点,若△
1(a>b>0)的一个焦点,且该抛物线的准线与椭圆相交于A、B两点,若△![]() FAB是等边三角形,则此椭圆的
FAB是等边三角形,则此椭圆的![]() 离心率为()
离心率为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、填空题(本大题共4小题,每小题5分,共20分)
13.曲线y=excosplayx在点(0,1)处的切线斜率为__________.
14.已知双曲线![]() 上一点P到它的一个焦点的距离为4,那样点P到另一个焦点的距离为__________.
上一点P到它的一个焦点的距离为4,那样点P到另一个焦点的距离为__________.
15.已知命题p:“∀x∈[1,2],x2+1≥a”,命题q:“∃x0∈R,x02+2ax0+1=0”,若命题“¬p∨¬q”是假命题,则实数a的取值范围是__________.
16.若函数f(x)=lnx![]() ax﹣b在概念域上是增函数,则实数a的取值范围是__________.
ax﹣b在概念域上是增函数,则实数a的取值范围是__________.
3、解答卷(本大题共6小题,共刊分解答应写出文字说明、证明过程或演算步骤)
17.求下列函数的导数:
(1)y=exlnx;
(2)y![]() .
.
18.已知数f(x)=﹣x3﹣6x2﹣9x+3.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求f(x)的极值.
19.已知抛物线C:y2=2px(p>0)的顶点在坐标原点,焦点为圆M:(x﹣2)2+y2=4的圆心.
(Ⅰ)求抛物线C的规范方程和准线方程;
(Ⅱ)若直线l:y=kx+b(k≠0)为物线C的切线,证明:圆心M到直线l的距离恒大于2.
20.已知命题p:m﹣1<a<m2+1;命题q:函数f(x)=log2x﹣a在区间(![]() ,4)上有零点.
,4)上有零点.
(Ⅰ)当m=1时,若(¬p)∧q为真命题,求实数a的取值范围;
(Ⅱ)若命题p是命题q的充分非必要条件,求实数m的取值范围.
21.已知椭C:![]() (a>b>0)的离心率e
(a>b>0)的离心率e![]() ,坐标原点O到直线l:y=bx+2的距离为
,坐标原点O到直线l:y=bx+2的距离为![]() .
.
(Ⅰ)求椭圆C的规范方程;
(Ⅱ)已知定点E(﹣1,0),若直线y=kx+2(k≠0)与椭圆C相交于不一样的两点A(x1,y1),B(x2,y2),且![]() 0,求k的值.
0,求k的值.
22.已知函数f(x)=alnx﹣3x在x![]() 处获得极值.
处获得极值.
(Ⅰ)若对任意x∈(0,+∞),f(x)≤m恒成立,求实数m的取值范围;
(Ⅱ)讨论函数F(x)=f(x)+x2+k(k∈R)的零点个数.
1、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目需要的
1.A
2.C
3.A
4.C
5.解![]() :焦点在y轴上的椭圆
:焦点在y轴上的椭圆![]() 1(a>0)的焦距为4
1(a>0)的焦距为4![]() ,
,
可得a2﹣4=12,解得a=4,
所以2a=8.
故选:B.
6.C
7.D
8.A
9.B
10.A
11.A
12.C
2、填空题(本大题共4小题,每小题5分,共20分)
13. 1.
14. 6.
15.(﹣∞,﹣1]∪[1,2].
16.由题意可知,x>0,且f′(x)![]() 0恒成立,
0恒成立,
∴a![]() 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
依据二次函数的性质可知,![]() 0,
0,
∴a≤0,即a的范围为(﹣∞,0].
3、解答卷(本大题共6小题,共刊分解答应写出文字说明、证明过程或演算步骤)
17.(1)y′=exlnx+ex![]() ex(lnx
ex(lnx![]() ).[来源:学科网]
).[来源:学科网]
(2)y′=(![]() )′
)′![]() .
.
18.(Ⅰ)∵f(x)=﹣x3﹣6x2﹣9x+3,
∴f′(x)=﹣3x2﹣12x﹣9,
由f′(x)<0,得x<﹣3或x>﹣1;由f′(x)>0,得﹣3<x<﹣1.
∴f(x)的单调递增区间为(﹣∞,﹣3),(﹣1,+∞),单调递减区间为(﹣3,﹣1).
(Ⅱ)∵f(x)的单调递减区间为(﹣∞,﹣3),(﹣1,+∞),
单调递增区间为(﹣3,﹣1),
∴f(x)极小值=f(﹣3)=3,f(x)很大值=f(﹣1)=7.
19.(Ⅰ)抛物线C:y2=2px(p>0)的焦点为(![]() ,0),准线方程为x
,0),准线方程为x![]() ,
,
圆M:(x﹣2)2+y2=4的圆心为(2,0),可得![]() 2,即p=4,
2,即p=4,
可得抛物线的方程为y2=8x,准线方程为x=﹣2;
(Ⅱ)证明:联立![]() 可得k2x2+(2kb﹣8)x+b2=0,
可得k2x2+(2kb﹣8)x+b2=0,
由题意可得△=(2kb﹣8)2﹣4k2b2=64﹣32kb=0,即kb=2,
圆心M(2,0)到直线y=kx+b的距离为d![]() 2
2![]() 2.
2.
20.(Ⅰ)当m=1时,命题p:0<a<2,则¬p:a≤0或≥2.
∵函数f(x)![]() =log2x﹣a在区间(
=log2x﹣a在区间(![]() ,4)上单调递增,
,4)上单调递增,
且函数f(x)=log2x﹣a在区间(![]() ,4)上有零点
,4)上有零点
∴log2![]() a<0且log24﹣a>0,∴﹣2<a<2,
a<0且log24﹣a>0,∴﹣2<a<2,
∴命题q:﹣2<a<2,
∵若(¬p)∧q为真命题,
∴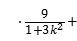 ,∴﹣2<a≤0
,∴﹣2<a≤0
∴实数a的取值范围是(﹣2,0].
(Ⅱ)∵命题p:m﹣1<a<m2+1;命题q:﹣2<a<2,命题p是命题q的充分非必要条件,
∴![]() ,得﹣1≤m≤1.
,得﹣1≤m≤1.
∵命题p是命题q的充分非必要条件,
∴m≠﹣1
∴实数m的取值范围(﹣1,1].
21.(Ⅰ)由题意得:e![]() ,a2=b2+c2,所以得:1
,a2=b2+c2,所以得:1![]() ,a2=3b2,坐标原点O到直线l:y=bx+2的距离为
,a2=3b2,坐标原点O到直线l:y=bx+2的距离为![]() ,所以
,所以![]() ,∴b2=1,a2=3,所以椭圆的C的规范方程为:
,∴b2=1,a2=3,所以椭圆的C的规范方程为:![]() y2=1;
y2=1;
(Ⅱ)由(Ⅰ)将直线方程与椭圆方程联立整理得:(1+3k2)x2+12kx+9=0,
△=36k2﹣36>0,k2>1,x1+x2![]() ,x1x2
,x1x2![]() ,
,![]() ,
,
所以![]() (x1+1,y1),
(x1+1,y1),![]() (x2+1,y2),
(x2+1,y2),![]() (x1+1)(x2+1)+y1y2=0,
(x1+1)(x2+1)+y1y2=0,
∴(1+k2)x1x2+(2k+1)(x1+x2)+5=0即(1+k2)![]() (2k+1)
(2k+1)![]() 5=0,
5=0,
解得:k![]() 1;
1;
所以k的值为:![]() .
.
22.(Ⅰ)∵![]() ,由题意,
,由题意,![]() ,
,
∴a=1,
∴![]() ,
,
当![]() 时,f′(x)<0,当
时,f′(x)<0,当![]() 时,f′(x)>0,
时,f′(x)>0,
∴函数f(x)在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,
上为减函数,![]() ,
,
∴m≥﹣ln3﹣1,即实数m的取值范围为[﹣ln3﹣1,+∞);
(Ⅱ)F(x)=f(x)+x2+k=lnx﹣3x+x2+k,x∈(0,+∞),
∴![]() ,
,
令F′(x)=0,解得![]() ,
,
当x变化时,F(x),F′(x)的变化状况如下表,
x | | | | 1 | (1,+∞) |
F′(x) | + | 0 | ﹣ | 0 | + |
F(x) | 递增 | 很大值 | 递减 | 极小值 | 递增 |
而![]() ,
,
∴当![]() 且﹣2+k<0,即
且﹣2+k<0,即![]() 时,函数F(x)有3个零点;
时,函数F(x)有3个零点;
当![]() 或﹣2+k=0,即
或﹣2+k=0,即![]() 或k=2时,函数F(x)有2个零点;
或k=2时,函数F(x)有2个零点;
当![]() 或﹣2+k>0,即
或﹣2+k>0,即![]() 或k>2时,函数F(x)有1个零点.
或k>2时,函数F(x)有1个零点.







